Skip navigation

Ingredient Calibration

In the Statement of the Theory section, a technique for calculating balanced cocktail recipes is proposed, which relies on knowledge of the flavor density vector \vec{\rho} for each ingredient.  So before that formalism can be used to predict cocktail recipes, some way of measuring \vec{\rho} for the ingredients of interest is required.  As far as I know, the only way of extracting this kind of information is to use known cocktail recipes to infer it.

Necessary Precision in Recipes

We will first consider a simple (but real) example.  I have personally tested several variations of the basic gin sour cocktail, using Tanqueray, and came to the conclusion that the most balanced recipe for my tastes is:

(1)   \begin{eqnarray*} \textnormal{\bf{Tanqueray Gin}} & 50 \; \textnormal{ml} & [1.667 \; \textnormal{oz}] \nonumber \\ \textnormal{\bf{Lemon Juice}} & 25 \; \textnormal{ml} & [0.833 \; \textnormal{oz}] \nonumber \\ \textnormal{\bf{Simple Syrup (1:1)}} & 20 \; \textnormal{ml} & [0.667 \; \textnormal{oz}]. \end{eqnarray*}

An example cocktail that I used the program to calculate.

The Gin Sour.

First of all, note the precision here.  While many cocktail recipes call generically for “gin”, here I’ve stated the brand explicitly.  This is because the flavor density vector of one gin brand may differ from another and we want to be mindful of that.  As for the simple syrup, the notation (1:1) means that it was made from equal parts sugar and water by volume.  I use caster sugar and dissolve it by cold shaking, as opposed to heating the water which may result in some evaporation after the volume measurement.  It’s worth mentioning, however, that I have not found any evidence that the recipe should change when the simple syrup is made by heating or when the caster sugar is replaced by raw cane sugar.  Also, note the amounts in this recipe are quoted in multiples of  5 ml, which is because this is the smallest unit that any jigger is capable of measuring (and only one jigger can do this: Oxo’s Mini Angled Measuring Cup).  All measurements are taken at eye level to avoid parallax error.  This brings the uncertainty in the volume of any ingredient to probably \sigma \sim 1 ml (or 1/5 of a teaspoon), which may seem like gilding the lily, but that means this recipe has ingredients with volume uncertainties of up to 5% and other recipes which call for even smaller amounts will have significantly higher uncertainties.  The precision on the volume is not even the only source of uncertainty!  If the true most balanced recipe actually required the lemon juice to be at 22.5 ml instead of 25 ml, we would not be sensitive to this with our measuring equipment (or maybe even our taste buds, in which case it would not matter); we could possibly detect this by making larger cocktails, but I’m not prepared to drink that much in one sitting or waste that much alcohol. In other words, the accuracy is limited by the requirement that all amounts be in discrete multiples of 5 ml coupled with the limitation that the test cocktails are of reasonable size (the total volume of alcoholic ingredients is generally kept below 70 ml).

A Note on Shaking

What about consistency in the shaking conditions? One might ask whether there will be some effect if someone uses different types of ice and shakes differently than I have. Thanks to the groundbreaking efforts of some cocktail science experimentalists (Shaking Study) we actually have an answer to this. As long as one uses a sufficient amount of ice and shakes for at least 12 seconds, the resulting cocktail temperature and dilution is independent of shaking style and the type of ice used to a very good approximation.

Inferring 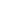\vec{\rho} and Defining Flavor Units

Moving on, since recipe 1 is a balanced cocktail, it must be a solution of Eq. 11 from Statement of the Theory.  This provides two equations of constraint for nine unknown parameters (3 ingredients, each with a 3 component vector of unknowns).  Fortunately, as will be typical for most ingredients, we can make some very well motivated assumptions about the form of \vec{\rho} for each ingredient, specifically:

(2)   \begin{eqnarray*} \vec{\rho}_{\textnormal{Tanqueray}} & = \left[ \begin{array}{c} \rho_{bite,T} \\ 0 \\ 0 \end{array} \right] \\ \vec{\rho}_{\textnormal{Lemon Juice}} & = \left[ \begin{array}{c} 0 \\ 0 \\ \rho_{sour, LJ} \end{array} \right] \\ \vec{\rho}_{\textnormal{Simple Syrup (1:1)}} & = \left[ \begin{array}{c} 0 \\ \rho_{sweet, SS} \\ 0 \end{array} \right]. \end{eqnarray*}

The assumptions that lemon juice only carries sourness and simple syrup only carries sweetness are fairly uncontroversial and were basically already assumed throughout much of the discussion in Statement of the Theory.  Tanqueray is a London Dry, which is a style of gin that is defined by its lack of sweetness, so it is very reasonable to assume that it only carries bite.  Keep in mind though, that this is not true of all spirits: rums and tequilas usually contain some element of sweetness.

Next, we will define units to measure flavor.  We will do this by setting \rho_{sour, LJ}=1 \frac{\textnormal{fl}}{\textnormal{oz}}, where fl is a unit of flavor defined such that lemon juice has one of it per oz.  This means that we are effectively measuring everything else in units of lemon juice.  We could have chosen something else as a reference to measure flavors against, but lemon juice ends up working quite well because it appears in quite a few recipes.

We can now plug all of this into Eq. 11 from Statement of the Theory (suppressing units):

(3)   \begin{equation*} 1.667 \rho_{bite,T} = 0.833 = 0.667 \rho_{sweet, SS} \end{equation*}

and solve for the complete flavor density vectors of Tanqueray gin and simple syrup (1:1):

(4)   \begin{eqnarray*} \rho_{bite,T} = 0.5 \; \textnormal{fl} / \textnormal{oz} \\ \rho_{sweet, SS} = 1.25 \; \textnormal{fl} / \textnormal{oz}. \end{eqnarray*}

We now have all of the information we need on these three ingredients to know how to mix them in other cocktails of the sour family.

If we repeat this kind of analysis on a larger collection of recipes involving a variety of ingredients, then we can eventually build a substantial database of information on flavor density vectors for all the ingredients we are interested in.  This is the basic idea behind Project Calcuhol.  I have written an algorithm that accepts a collection of ingredients with assumptions about the form of their flavor density vectors as in Eq. 2 and a set of recipes involving them.  When the same ingredient appears in multiple recipes, this means we get multiple measurements of its \vec{\rho}, which presents opportunities to (1) reduce the uncertainty in \vec{\rho} by averaging them and (2) to in fact test the validity of the model itself.  This latter point is very interesting and I hope to revisit it at some point.  In principle, with enough independent measurements of \vec{\rho} for some ingredient, one could see a statistical distribution that could reveal aspects about the model.  At the moment, all of the recipe data is coming from my own personal, pain-staking, taste tests.  There is, of course, a vast amount of recipe data available in books and the internet; however,  I find it problematic because I usually have to tweak them quite a bit to my tastes, and some recipes are downright awful.  Published recipes typically don’t make the spirit brand specific and many times do not specify the proportions in the simple syrup.  Also,  when you look through a recipe book, even a good one, I think that you are seeing cocktails that span a variety of different personal tastes (perhaps contributions from many different bartenders).  Our model really works best if we can keep it focused on one set of personal tastes.

Leave a Reply